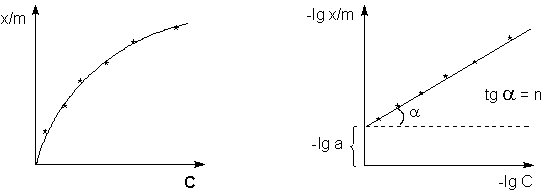Кафедра физхимии ЮФУ (РГУ) - Практикум по физколлоидной химии

Кафедра физхимии ЮФУ (РГУ)

ПРАКТИКУМ ПО ФИЗИЧЕСКОЙ И КОЛЛОИДНОЙ ХИМИИ

для студентов биолого-почвенного факультета

Работа № 6
АДСОРБЦИЯ УКСУСНОЙ КИСЛОТЫ НА АКТИВИРОВАННОМ УГЛЕ

Задания к работе

1. Приготовить серию растворов уксусной кислоты с заданными концентрациями.

2. Определить равновесную концентрацию при адсорбции на активированном угле для каждого из растворов.

3. Построить графики изотермы адсорбции в обычных и логарифмических координатах.

4. Определить коэффициенты уравнения Фрейндлиха.

Описание работы

В шести пронумерованных конических колбах объемом 250 мл разбавлением 0.8 М раствора уксусной кислоты готовят рабочие растворы СН₃СООН в соответствии с указанным преподавателем номером задания (табл. 1).

Для приготовления растворов при помощи мерного цилиндра (с точностью до 1 мл) наливают в каждую колбу рассчитанное по формуле (1) количество 0.8 М раствора уксусной кислоты и доливают необходимое количество дистиллированной воды.

(1)

Здесь С_x и V_x - концентрация и объем приготовляемого раствора;
V_0.8 - необходимый объем 0.8 М раствора СН₃СООН.

Таблица 1

Номер задания	Приблизительная концентрация приготовляемых растворов, моль/л
Номер задания	1	2	3	4	5	6
1 2 3 4 5 6	0.01 0.01 0.01 0.01 0.02 0.02	0.02 0.02 0.03 0.03 0.04 0.03	0.04 0.05 0.06 0.07 0.08 0.08	0.08 0.10 0.12 0.15 0.16 0.12	0.16 0.20 0.24 0.30 0.32 0.25	0.32 0.40 0.36 0.40 0.40 0.40
Объём, мл	150	150	150	125	110	105

Точную концентрацию приготовленных растворов определяют титрованием 0.1 М раствором NаОН. Для этого в колбы из второго комплекта с соответствующим номером отбирают из колб №№ 1-3 по 50 мл, из колбы № 4 - 25 мл, из колбы № 5 - 10 мл и из колбы № 6 - 5 мл раствора (т.е. такое количество, чтобы во всех колбах оставалось по 100 мл раствора). После титрования точную концентрацию приготовленных растворов вычисляют по формуле (2):

(1)

Здесь С_щел и V_щел - концентрация и объем раствора щелочи, затраченного на титрование пробы;
V_к-ты - объем пробы, взятой для титрования.

В каждую из колб со 100 мл раствора вносят указанное преподавателем количество растертого в ступке активированного угля, энергично перемешивают и оставляют на 30 минут, в течении которых содержимое колб периодически взбалтывают (это время можно использовать для титрования отобранных проб). По истечении получаса растворы профильтровывают через складчатые фильтры (первую порцию фильтрата необходимо отбросить, чтобы устранить погрешность, вносимую адсорбцией кислоты на фильтровальной бумаге и разбавлением раствора остающимися в колбе каплями воды). Из фильтрата отбирают пробы такого же объема, что и ранее, титруют их раствором щелочи и рассчитывают концентрацию растворов кислоты после адсорбции.

По формуле (6.3) вычисляют х - количество миллимолей уксусной кислоты, адсорбированной активированным углем и рассчитывают величину удельной адсорбции x/m (m - масса активированного угля) для каждого из растворов.

, ммоль/г (3)

Здесь С_о - концентрация исходного раствора;
С - концентрация раствора после адсорбции.

Адсорбция уксусной кислоты на активированном угле описывается уравнением Фрейндлиха:

(4)

После логарифмирования выражения (4) получается линейная функция (5):

(5)

Рисунок 1. Изотерма адсорбции

Рисунок 2. Изотерма адсорбции
в логарифмических координатах.

Полученные данные заносят в таблицу 1 и строят на миллиметровой бумаге изотерму адсорбции, откладывая по оси абсцисс концентрации растворов после адсорбции С, а по оси ординат - значения удельной адсорбции (рис.1).

Для определения коэффициентов в эмпирическом уравнении Фрейндлиха (4) строят изотерму адсорбции в логарифмических координатах (рис. 2). При этом отрезок, отсекаемый на оси ординат, равен lg a, а тангенс угла наклона прямой к оси абсцисс - показателю степени n.

Таблица 2

№ колбы	С_o, моль/л	С, моль/л	х, ммоль	x/m, ммоль/г	lg C	lg (x/m)

Другие работы:
№ 1. Калориметрическое определение теплоты растворения
№ 2. Определение константы скорости и энергии активации реакции
№ 3. Измерение ЭДС гальванического элемента
№ 4. Потенциометрическое определение рН растворов
№ 5. Определение поверхностного натяжения растворов ПАВ
№ 6. Изучение адсорбции уксусной кислоты на активированном угле
№ 7. Получение коллоидных растворов. Определение порога коагуляции
№ 8. Определение электрокинетического потенциала золя

В начало страницы