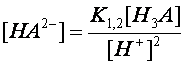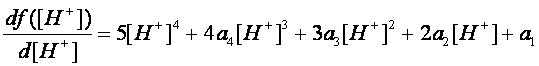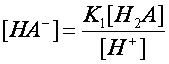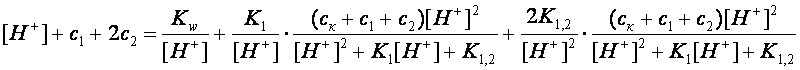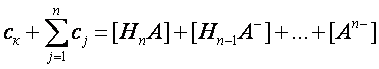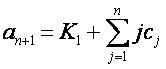|
ЧИСЛЕННЫЕ МЕТОДЫ И ПРОГРАММИРОВАНИЕ Материалы к лекционному курсу Лектор – ст. преп. Щербаков И.Н. Моделирование состава раствора слабой трехосновной кислоты. 1. Построение описательной модели. В водном растворе слабая кислота H3A подвергается ступенчатой диссоциации: 1-я ступень диссоциации: 2-я ступень диссоциации
3-я ступень диссоциации
Здесь K1,2 = K1K2, K1,3 = K1K2K3 Кроме этого, в растворе протекает автопротолиз воды из уравнения материального баланса по аниону следует
после подстановки приведенных выше выражений можно получить равновесную концентрацию недиссоциированной кислоты
Теперь запишем уравнение закона сохранения заряда –
и подставим в него полученные выражения для равновесных концентраций. В результате, приходим к уравнению относительно концентрации ионов водорода. После приведения подобных членов получается алгебраическое уравнение 5-й степени
Полученное уравнение легко решается численно методом Ньютона (касательных), так как производная левой части уравнения f’([H+]) легко выражается через те же самые коэффициенты ai., что и f([H+])
Решив полученное уравнение, равновесные концентрации остальных компонентов рассчитывают по приведенным выше формулам. Моделирование состава буферного раствора слабой двухосновной кислоты. Равновесие в буферном растворе, содержащем слабую двухосновную кислоту H2A концентрации cк, кислую соль NaHA концентрации c1 и среднюю соль Na2A концентрации c2 может быть описано аналогично приведенному выше примеру. Из ЗДМ для двух стадий ступенчатой диссоциации получим:
из уравнения материального баланса по аниону
после подстановки этих выражений равновесная концентрация недиссоциированной формы кислоты записывается:
Теперь воспользуемся выражением закона сохранения заряда, учитывая, что соли диссоциируют нацело и концентрации катионов натрия будут равны с1 для кислой соли и 2с2 для средней соли, соответственно.
После подстановки получим следующее выражение, являющееся уравнением относительно равновесной концентрации ионов водорода [H+]
После приведения подобных членов получается алгебраическое уравнение 4-й степени
Моделирование состава буферного раствора слабой n-основной кислоты и соответствующих солей. Рассмотрим задачу о составе буферного раствора слабой кислоты и соответствующих солей в наиболее общем виде. Пусть раствор содержит слабую n-основную кислоту HnA концентрации cк, однозамещенную соль NaHn-1A концентрации c1 , двузамещенную соль Na2Hn-2A концентрации c2 и т.д., среднюю соль NanA концентрации cn. Тогда в растворе будет находится в равновесии (n+3) компонента. n равновесий ступенчатой диссоциации, равновесие автопротолиза воды, закон сохранения вещества по аниону
и закон сохранения заряда
образуют ровно (n+3) уравнения для определения равновесных концентраций всех компонентов. Аналогично рассмотренным ранее примерам, задача сводится к алгебраическому уравнению степени n+2 относительно равновесной концентрации ионов водорода с коэффициентами:
для всех i от 2 до n.
При подстановке следует учитывать, что K1,0 = 1,
K1,1= K1,
K1,2= K1 K2, …, |