Главная
страница
 
Учебные
материалы
 
Программа
курса

Виктор Александрович КОГАН
профессор, заведующий кафедрой физической и коллоидной химии
Ростовского Государственного Университета

 
ИЗБРАННЫЕ ЛЕКЦИИ ПО КУРСУ "МЕТОДЫ ИССЛЕДОВАНИЯ КООРДИНАЦИОННЫХ СОЕДИНЕНИЙ"

 
Метод дипольных моментов в химии

Лекция посвящена одному из важнейших физических методов исследования строения вещества – методу дипольных моментов. Рассмотрена природа дипольного момента и методы его определения, а также приведены отдельные примеры применения метода дипольных моментов для выяснения строения химических соединений.

 
1. Общие представления о природе дипольного момента

Дипольный момент – важная молекулярная константа, характеризующая электрическую симметрию молекулы.

Знание величины дипольного момента необходимо для изучения природы химической связи, оценки прочности донорно-акцепторных и межмолекулярных связей, для квантово-химических расчетов. По величине дипольного момента можно судить об изомерии и конформации органических соединений, конфигурации координационных узлов комплексов, о взаимном влиянии атомов и связей в молекуле.

Величина электрического дипольного момента (μ) определяется соотношением:

                                           (1)

где l - радиус-вектор, направленный от центра тяжести отрицательного электрического заряда к центру тяжести положительного заряда, абсолютная величина каждого заряда равна q. В химической литературе, так же как и в настоящей лекции, принято противоположное направление вектора дипольного момента. По порядку величины дипольный момент в системе CGSE равен заряду электрона (4.8·10^-10 эл.-ст. ед.), умноженному на расстояние в 1Å (10^-8 см), что составляет 4.8·10^-18 эл.-ст. ед. Принято измерять дипольные моменты в единицах Дебая: 1 D = 1·10^-18 эл.-ст. ед. В системе единиц СИ 1 D = 3.34·10^-30 Кл*м.

Причиной появления дипольного момента являются несколько факторов. В первую очередь – это различия в природе составляющих молекулу атомов. В простейшем случае для двухатомной молекулы μ = 0, если она состоит из двух одинаковых атомов. Это относится к H₂, O₂, N₂ и т.д. В двухатомной молекуле с атомами разной природы проявляется постоянный дипольный момент, т. к., вследствие разной электроотрицательности, характеризующей способность атома оттягивать электронную плотность, появляется асимметрия электронной плотности. Другие причины – разные гибридные состояния орбиталей атомов. Так, например, для связи H-Cl, образованной 1s-орбиталью водорода и 3p-орбиталью хлора, вследствие различной формы s- и p-орбиталей, центр тяжести заряда перекрывания смещен в сторону водорода на ΔL, за счет чего возникает дополнительный, т. н. гомеополярный дипольный момент (рис.1):

Рис. 1. Схема происхождения гомеополярного диполя.

 
Естественно, молекулы HCl, HBr, HI имеют постоянные дипольные моменты, равные, соответственно, 1.95 D, 0.79 D, 0.40 D. Другие вклады в суммарный дипольный момент возникают из-за асимметрии связывающей и несвязывающей атомных орбиталей вследствие их гибридизации. Так, дипольный момент аммиака, 1.46 D, в основном обусловлен моментом несвязывающей пары электронов азота.

 
2. Методы определения дипольных моментов

Методы определения дипольных моментов основаны на нахождении ориентационного эффекта (за исключением метода молекулярного пучка) полярных молекул в приложенном электрическом поле. При этом следует учитывать, что если молекула является полярной и обладает дипольным моментом, то он называется постоянным или собственным дипольным моментом (μ_o). А при поляризации молекул в электрическом поле возникает индуцированный дипольный момент молекулы (μ_g). В статических полях или полях с относительно низкими частотами колебаний происходит поляризация вещества в целом, включающая также некоторое смещение ядер и ориентацию молекул вдоль поля, и возникает индуцированный ориентационный дипольный момент молекул (μ_r), который зависит от μ_o и из которого можно определить постоянный дипольный момент молекулы μ_o. Для точных измерений μ_o малых молекул применяются методы, основанные на микроволновой спектроскопии и молекулярных пучков. Особенно распространен метод Штарка, основанный на эффектах расщепления и сдвига спектральных линий в электрическом поле. Для линейных молекул известны точные выражения, связывающие дипольный момент со штарковским расщеплением линий вращательных спектров. Этот метод дает наиболее точные значения величины дипольного момента (до 10^-4 D), причем экспериментально определяется не только величина, но и направление вектора дипольного момента. Важно, что точность определения дипольного момента почти не зависит от его абсолютной величины. Это позволило получить весьма точные значения очень малых дипольных моментов ряда молекул углеводородов, которые нельзя надежно определить другими методами. Так, дипольный момент пропана равен 0.085±0.001 D, пропилена – 0.364±0.002 D, пропина – 0.780±0.001 D, толуола – 0.375±0.01 D, азулена – 0.796±0.01 D. Область применения метода микроволновой спектроскопии ограничена небольшими молекулами, не содержащими атомов тяжелых элементов.

Из всех методов получили наиболее широкое распространение методы определения дипольных моментов, основанные на измерении диэлектрической проницаемости (ε) вещества. Этими методами измерены дипольные моменты молекул более 10000 веществ. Переход от измеряемого значения ε газа, чистой жидкости или разбавленного раствора, т.е. макроскопической характеристики диэлектрика, к величине дипольного момента основан на теории поляризации диэлектриков. Считается, что при наложении электрического поля на диэлектрик его полная поляризация Р складывается из наведенной или индуцированной поляризации Р_м и поляризации Р_ор и связана с μ уравнением Ланжевена-Дебая (2).

                      (2)

где М – молекулярная масса, d – плотность, α - поляризуемость молекулы, N_A - число Авогадро, k – постоянная Больцмана, Т – абсолютная температура.

 
Измерения диэлектрической проницаемости проводят в постоянном поле или при низких частотах, обеспечивающих полную ориентацию молекул по полю. Кратко остановимся на типичной процедуре определения μ_о в разбавленных растворах. Она основана на предположении об аддитивности свойств составляющих раствор компонентов:

                          (3)

где Р_1,2, Р₁, Р₂ – молекулярные поляризации раствора, растворителя и растворенного вещества соответственно;
Х₁, Х₂ – мольные доли растворителя и растворенного вещества.

С учетом уравнения (2) уравнение (3) для раствора будет выглядеть как (4):

                          (4)

где М₁ и М₂ – молекулярные веса растворителя и растворенного вещества;
ε_1,2 – диэлектрическая проницаемость раствора;
d_1,2 – плотность раствора.

 
Из уравнения (4) можно вычислить Р₂ – молекулярную поляризацию растворенного вещества. В этом методе допускается, что молекулы полярного вещества могут вести себя в растворах как в парообразном состоянии и свободно ориентироваться в приложенном поле только для бесконечно разбавленных растворов, поэтому значение Р₂ следует экстраполировать на нулевую концентрацию (Х₂ = 0) и найти значение молекулярной поляризации растворенного вещества при бесконечном разбавлении (Р_2∞).

Эксперимент сводится к измерению диэлектрической проницаемости и плотности 5-7 разбавленных растворов исследуемого соединения при точно поддерживаемой температуре (обычно 25 °С) в интервале концентраций растворенного вещества от 0,001¸ 0,01 мольных долей. Выбор интервала концентраций зависит от растворимости и полярности вещества и может колебаться в сторону уменьшения мольных долей для более полярных соединений. Затем по формуле (4) находят значение молекулярной поляризации растворенного вещества для каждой концентрации и по полученным данным строят кривую зависимости Р₂ от концентраций, по которой экстраполируют Р₂ до нулевой концентрации и находят значение Р_2∞. Эту величину можно также получить, используя различные приемы экстраполяции к нулевой концентрации для диэлектрической проницаемости и плотности.

Величину дипольного момента рассчитывают из уравнения Дебая (2)

из которого, подставляя значения N, κ, π, можно вычислить величину постоянного дипольного момента по формуле (5):

, эл.-ст. ед.                      (5)

Найденное в эксперименте значение Р_2∞ включает в себя электронную (Р_эл) и атомную (Р_ат) молекулярные поляризации и поэтому Р_ор в уравнении (5) вычисляется как Р_ор = Р_2∞ – Р_ат – Р_эл.

Р_эл считают равной рефракции вещества, которое вычисляется по той же схеме аддитивности на основании измерения коэффициентов преломления и плотности той же серии растворов, а Р_ат вследствие ее малости очень часто пренебрегают. Следует отметить, что Р_эл можно рассчитать по рефракциям связей и групп, если не требуется высокая точность в значении дипольного момента.

Сходимость результатов, полученных различными методами при корректном использовании правильных расчетных формул бывает достаточно хорошей, как показано в табл. 1:

Таблица 1. Дипольные моменты молекул (в D)

 
3. Расчетный аппарат метода дипольных моментов

Исследование большинства структурных проблем, проводимое с помощью данных о дипольных моментах молекул, основывается на сопоставлении экспериментальных величин дипольных моментов с величинами, рассчитанными по аддитивной схеме. Принципиальная идея последней была предложена в 1923 году Томсоном, который указал, что дипольный момент многоатомной молекулы m можно рассматривать как результат векторного сложения дипольных моментов, принадлежащих отдельным связям. Для молекулы, содержащей n связей различных типов,

                                       (6)

где μ_i – момент, характеризующий i-ю связь.

 
Дипольные моменты связей и групп, в свою очередь, находят или путем теоретической оценки из квантово-химических расчетов, или полуэкспериментальными методами из интенсивностей колебательных полос поглощения, либо путем векторного сложения дипольного момента некоторых симметричных молекул. В последнем случае уравнение (6) может быть использовано для решения обратной задачи: разложения суммарного дипольного момента на составляющие. Например, моменты связей H-O и H-N можно вычислить из значений дипольных моментов воды и аммиака соответственно:

2 μ_O-H cos 52° = 1.84 D.                                    3 μ_N-H cos 68° = 1.46 D.
μ_O-H = 1.51 D.                                                  μ_N-H =1.31 D.

 
Основой системы дипольных моментов связей является величина момента связи C-H метильной группы, которая, по расчитанным и экспериментальным данным, в том числе и по данным ИК-спектров, была принята за величину, близкую к 0.4 D. Вместе с тем, всегда следует учитывать гибридное состояние атома углерода, при котором находится протон. По данным ИК-измерений были установлены следующие значения моментов связей: C_sp3 – H⁺ = 0.31 D; C_sp2 – H⁺ = 0.63 D; C_sp – H⁺ = 1.05 D. Соответственно будут меняться моменты связей С-С с различными гибридными состояниями атома углерода и дипольные моменты молекул в целом. Во многих случаях удобнее пользоваться не моментами связей, а моментами отдельных групп. Например, при анализе дипольного момента ароматических нитросоединений нет необходимости учитывать отдельные моменты связей C-N, N=O, N→O, а целесообразно ввести результирующую величину группового момента μ_NO2. При этом μ_NO2 принимается равным дипольному моменту бензола и, следовательно, является фактически суммой моментов нитрогруппы и C-H-связи в п-положении. Это очень удобно, т. к. позволяет исключить введение в расчеты в явном виде моментов связей C-H. Действительно, дипольный момент м-нитробензола, например, можно рассчитать просто как векторную сумму двух моментов μ_NO2.

Имеются таблицы групповых моментов, где за величину группового момента в ароматическом ряду принимается значение дипольного момента монозамещенного бензола, а в алифатическом – соответствующего монозамещенного метана. В таблице 2 в качестве примера приведены лишь некоторые групповые моменты.

Таблица 2. Групповые моменты (бензол, 25 оС).

Θ - угол между вектором группового момента и связью Х-С.

 
Групповые моменты часто используются в расчетах для различных целей. Для молекул, содержащих две жестко закрепленные полярные группы, расчет дипольного момента молекулы (μ) сводится к сложению двух векторов(μ₁ и μ₂), находящихся друг к другу под некоторым углом φ:

                                (7)

Более сложным метод расчета выглядит для молекул, содержащих произвольное число жестко закрепленных полярных групп. Для них чаще всего применяется способ расчета  через проекции вектора дипольного момента на произвольно выбранные оси координат (8):

                                (8)

При этом под m_x, m_y, m_z подразумеваются суммы проекций на эту ось векторов всех групповых моментов. В качестве примера рассмотрим расчет дипольного момента 4,5-дихлор-1,3-бис-трифторметил-бензола:

CF₃ (1) m_x = 2.54 *;  m_y = 0.
CF₃ (3) m_x = -2.54 cos 60º;  m_y = 2.54 sin 60º.
Cl (4) m_x = -1.59;  m_y = 0.
Cl (5) m_x = -1.59 cos 60º;  m_y = -1.59 sin 60º.
------------------------------------------------------------
Σ m_xi = -1.12 D.   Σ m_yi = 0.83 D.

μ_выч = [ (-1.12)² + 0.832 ]^1/2 = 1.40 D

* Положительное значение m связи указывает на то, что m связи направлен по оси координат, а отрицательное – против.

 
Опытные значения по различным источникам составляют 1.51-1.62 D.

Естественно, если молекулы неплоские, то следует найти проекции векторов на соответствующие плоскости. Существенно усложняется расчет, если молекула содержит несколько свободно или заторможенно вращающихся полярных групп. Здесь применяются специальные подходы, описанные в монографиях.

Если молекулы некоторых соединений существуют в растворах или в газовой фазе в виде равновесной смеси двух или нескольких молекулярных форм: таутомеров, конформеров, мономеров и димеров, то экспериментально определяемый дипольный момент является в этом случае усредненной величиной. связанной с дипольными моментами индивидуальных форм соотношением (9):

                                (9)

где N_i и μ_i – соответственно мольные доли и дипольные моменты таутомера, конформера и др.

 
Расчет по формуле (9) можно иллюстрировать примером вычисления эффективного дипольного момента 2,5-диметокси-нитробензола, для которого показана возможность существования в растворе четырех равновероятных плоских конформаций I - IV:

μ_выч = 3.47 D.              μ_выч = 5.59 D.              μ_выч = 4.01 D.                μ_выч = 4.01 D.
I                                     II                                  III                                    IV

Воспользовавшись значениями групповых моментов из таблицы 2 и рассчитав теоретические величины дипольного момента каждого конформера, получим:

μ₂ = 0.25 (3.47)² + 0.25 (5.59)² + 0.25 (4.01)² + 0.25 (4.01)²

μ = 4.34 D.

Полученное значение близко к опытной величине 4.56 D (бензол, 18 °С)

Читать дальше:
Часть 4. Дипольные моменты и строение химических соединений

 
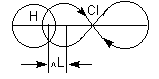
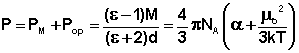Copyright  ©  В. А. Коган, 2005.

В начало страницы